This is a brief introduction on neutron stars that I have written for some high school students. I thought to share this with everyone, but keep in mind this is very basic material where sometimes I have favored intuition over a rigorous description of facts. Comments are welcome (as always). 

Neutron stars can be used to study all four fundamental forces of nature (gravity, electromagnetic, weak and strong force) operating in extreme conditions which cannot be reproduced in any Earth-based laboratory. This is very different from a black hole, which is a purely gravitational phenomenon (but see the recent discussion on Hawking radiation and quantum information paradox).

But what are neutron stars? Neutron stars are objects of the extreme: they are stellar remnants left after supernovae explosions and are the densest objects that can be directly observed in the Universe. Their density is so high that you need to squeeze the  Empire State Building into a small sphere about the size of a bunch of pixels on your laptop. Some neutron stars also possess the strongest magnetic fields in existence, which are about a million billion times stronger than the magnetic field of the Earth.

The size of a neutron star is startling: their mass is similar to that of the Sun (about 1-2 times) but their radius is just about 10 kilometers! This is the reason why they are so dense and indeed if you keep compressing them you would obtain a black hole quite rapidly. Neutron stars are also unique laboratories to test theories of gravity in the strong-field regime. Their surface gravitational (potential) energy is the highest known among directly observable objects: only black holes have larger gravitational fields close to their event horizons. However, in contrast to black holes, neutron stars have a solid surface that is directly observable by the distant observer. Since their surface gravity is high, gas flowing close to the neutron star’s surface approaches the speed of light, giving rise to Special relativistic effects.

Neutron stars are also the objects with the fastest rotational velocity in the Universe. Most of them rotate in one second or so, whereas in some extreme cases they can spin in about one millisecond. This means that their equator is rotating with a velocity that is a good fraction of the speed of light.

When they are born, their temperature can be as high as a hundred billion degrees (for comparison, the Sun has a surface temperature of 5500 K, whereas at its center the temperatures reach “just” 10 million degrees) and some systems can shine as much as a hundred thousand suns.

The Structure of a Neutron Star.

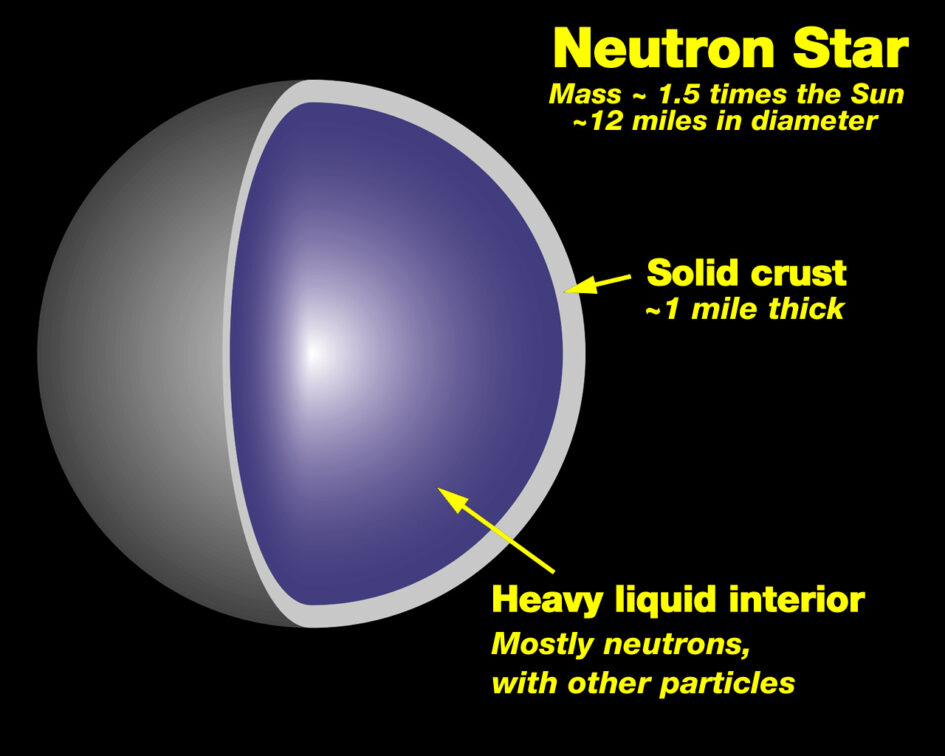
The neutron star structure can be split into four main layers (see Figure below). An outer crust, starting from the surface and with a thickness of a few hundred meters, is composed of atomic nuclei and free electrons. The density there is just one ton per cubic centimeter. The next layer is the inner crust, where free neutrons add to the atomic nuclei and free electrons form a very dense solid layer. Deeper down there is an outer (liquid) core, where free electrons, neutrons, protons, and muons co-exist in a nuclear soup. Finally, at the bottom of the outer core, the density grows so much that describing the particle interaction becomes problematic since our knowledge of the strong force is limited at these densities [remember that the strong force is responsible for the interaction between quarks in nucleons and also for the existence of the nuclear force that keeps atomic nuclei together]. This point marks the beginning of the inner core, a mysterious zone where elementary particles behave in an unpredictable way. The inner core of neutron stars is the densest point of the observable Universe, probably reaching values of about a billion tons per cubic centimeter…

figure23-09

Ultra-Dense Matter

At such enormous densities the properties of such ultra-dense matter are very uncertain and the understanding of its equation of state remains a major challenge for both theorists and experimentalists. In physics the term equation of state of matter refers formally to the relation between density,pressure and temperature of a certain material. For example, we know very well the equation of state of real gases, so we can easily calculate the pressure of the air in a room given its temperature and density. However, the equation-of-state of ultra-dense matter is completely unknown. In other words, the term is used to indicate the type of particles that compose the inner neutron star cores (e.g., are these particles protons+neutrons? Or are they free quarks? Or Bose-Einstein condensate? Or something else?). The properties of a specific equation of state at such tremendously high densities are completely determined by the (unknown) behavior of the strong force at these density regimes. Therefore if we could determine in some way the equation f state of ultra-dense matter we would immediately understand how the strong force behaves in a new regime of physics so far completely unexplored. Relatively little is currently known about ultra-dense matter with almost all the information we have coming from astrophysical observations more than direct lab experiments.

How to Determine the Neutron Star Composition.

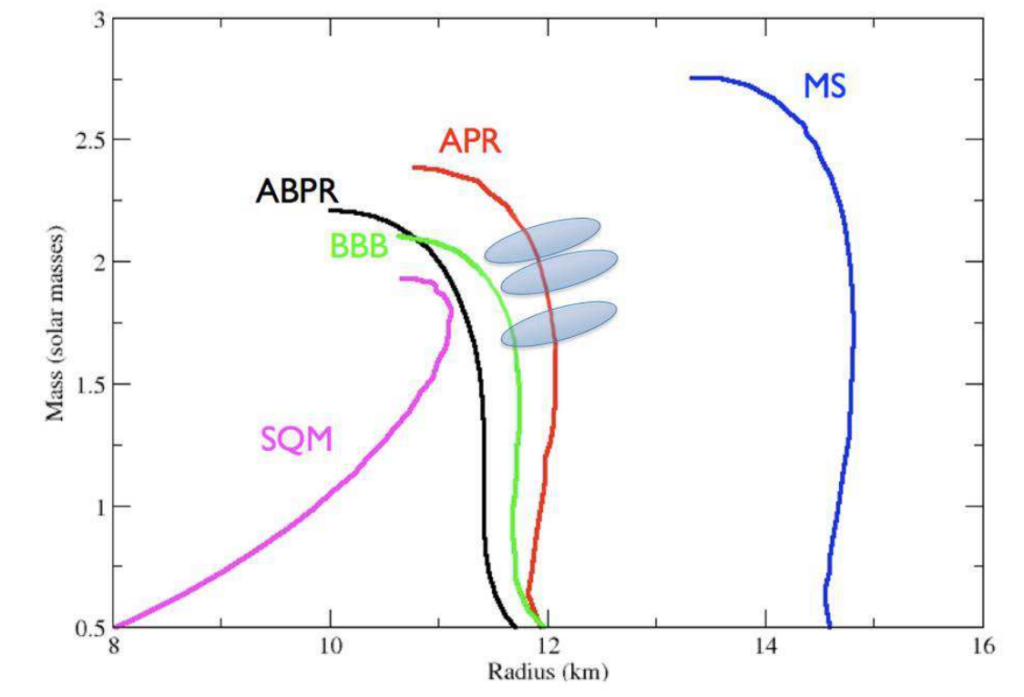
To determine the equation of state of ultra-dense matter (i.e., which particles compose the inner core of neutron stars) it is sufficient to measure the mass and radius of a neutron star. Why it is so? The kind of particle that appear in the inner core are determined by the density of the material there. The density of the material mainly depends on two factors: how much gravity there is and how intense the pressure that matter can generate to oppose the gravitational force. We know that the gravitational force is proportional to the mass of an object and inversely proportional to its radius squared (in first approximation, without invoking the theory of General Relativity). When the neutron star is forming after a supernova explosion there is a shell of matter that is collapsing. This means that the gravitational force is pulling the matter towards the center in a shrinking process. The more the matter shrinks the higher the gravitational force and the faster the collapse. At some point, however, the matter is so compressed that its pressure is so tremendously high that it stops the collapse leading to the formation of a neutron star with a certain specific final radius. This total pressure depends on the particle composition and therefore given a certain behavior of the strong force (i.e., given a certain particle composition of the inner core, or in other words, given a certain equation of state) the structure of the neutron star will change.  This means that if you pick a certain neutron star mass, then gravity will be balanced by pressure at a certain radius, which depends on the equation of state of ultra-dense matter. For a given mass, pick a different equation of state and you’ll get a different radius. This is why it is so important to measure both the mass and radius of neutron stars. In the Figure below there are a few neutron star mass-radius relationships and each curve refers to a different equation of state (labeled with the acronyms you see in the plot). It is clear that with a specific equation of state one can generate a curve that tells you the radius of a neutron star for a given mass. The blue ellipses show the hypothetical measurement of a neutron star’s mass and radius in three different objects. One curve (the APR one) crosses all three hypothetical measurements and therefore in that case we would immediately identify the APR equation of state as the true one for ultra-dense matter.

 

Something Funny

Neutron star equation of state examples.

facebookShare on Facebook
TwitterTweet
FollowFollow us
PinterestSave